| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 포스코 채용
- 과제형 코딩테스트
- Image Generation
- diffusion models
- Generative Models
- controlNet
- 코딩테스트
- stable diffusion
- 포스코 코딩테스트
- KT
- classifier-free guidance
- dp
- posco 채용
- colorization
- ip-adapter
- 논문 리뷰
- manganinja
- ddim
- DDPM
- kt인적성
- 프로그래머스
- Today
- Total
Paul's Grit
[논문 리뷰] [DDIM] Denoising Diffusion Implicit Models 본문
Jiaming Song, Chenlin Meng & Stefano Ermon
Stanford University
ICLR 2021 [Paper]
Abstract
Denoising Diffusion Probabilistic Models, DDPM은 샘플을 생성하기 위해 다수의 단계에서 마르코프 체인(Markov chain)을 시뮬레이션해야 한다는 단점이 있다. 샘플링 속도를 향상시키기 위해, 본 논문에서는 DDPM와 동일한 학습 절차를 따르는 보다 효율적인 iterative implicit probabilistic models인 Denoising Diffusion Implicit Models, DDIM을 제안한다.
DDPM에서는 생성 과정이 특정한 Markovian diffusion process의 역방향 과정으로 정의된다. 본 논문에서는 동일한 학습 목표를 유지하면서 non-Markovian 확산 과정의 한 범주를 통해 DDPM를 일반화한다. 이러한 non-Markovian 확산 과정은 deterministic generative processes에 해당할 수 있으며, 고품질 샘플을 훨씬 빠르게 생성하는 암시적 모델을 가능하게 한다.
실험적으로, DDIM는 DDPM에 비해 wall-clock time 기준으로 10배에서 50배 빠르게 고품질 샘플을 생성할 수 있으며, 계산량과 샘플 품질 간의 trade-off이 가능하고, latent space에서 의미론적으로 유의미한 image interpolation을 직접 수행할 수 있으며, 매우 낮은 오류로 관측값을 복원할 수 있음을 입증한다.
1 Introduction
Iterative generative models에 관한 최근 연구는 denoising diffusion probabilistic models, DDPM 및 noise conditional score networks, NCSN과 같은 모델이 adversarial training 없이도 GAN와 비교할 만한 품질의 샘플을 생성할 수 있음을 보여주었다.
이러한 모델들의 중요한 단점은 고품질 샘플을 생성하는 데 많은 반복(iterations)이 필요하다는 점이다. DDPM의 경우, 생성 과정(noise to data)이 순방향 확산 과정(data to noise)의 역방향을 근사하는 방식으로 이루어지는데, 이 과정은 수천 개의 단계로 구성될 수 있다. 따라서 모든 단계를 반복해야 하나의 샘플을 생성할 수 있으며, 이는 네트워크를 한 번만 통과하면 되는 GAN보다 훨씬 느리다.
DDPM와 GAN 사이의 효율성 차이를 줄이기 위해, 본 논문에서는 denoising diffusion implicit models (DDIM)을 제안한다. DDIM는 implicit probabilistic models로서, DDPM와 밀접한 관련이 있으며 동일한 목적 함수로 학습된다는 점에서 유사하다.
Section 3에서는 DDPM에서 사용되는 마르코프 확산 과정(Markovian diffusion process)을 비마르코프(non-Markovian) 과정으로 일반화하며, 이에 대해 적절한 역방향 생성 마르코프 체인(reverse generative Markov chain)을 설계할 수 있음을 보인다. 또한, variational training objectives가 공통된 대리 목표(surrogate objective)를 가지며, 이는 DDPM을 학습하는 데 사용되는 목적 함수와 정확히 일치함을 증명한다. 따라서 동일한 신경망을 사용하면서도 단순히 다른 비마르코프 확산 과정(Section 4.1)과 이에 대응하는 역방향 생성 마르코프 체인을 선택하는 것만으로 다양한 생성 모델을 자유롭게 선택할 수 있다. 특히, 적은 단계만으로 시뮬레이션이 가능한 "짧은" 생성 마르코프 체인(Section 4.2)을 유도하는 비마르코프 확산 과정을 활용할 수 있으며, 이는 샘플 품질의 약간의 손실만을 감수하면서도 샘플링 효율을 크게 향상시킬 수 있다.
Section 5에서는 DDIM가 DDPM에 비해 갖는 여러 실험적 이점을 보여준다. 첫째, 제안된 방법을 사용하여 샘플링 속도를 10배에서 100배까지 가속했을 때도 DDIM는 DDPM보다 우수한 샘플 생성 품질을 유지한다. 둘째, DDIM의 샘플은 DDPM에서는 성립하지 않는 "일관성(consistency)" 특성을 가진다. 즉, 동일한 초기 잠재 변수(latent variable)에서 시작하여 다양한 길이의 마르코프 체인을 사용해 여러 샘플을 생성하더라도, 이 샘플들은 유사한 high-level features을 공유한다. 셋째, DDIM의 "일관성" 덕분에, 초기 잠재 변수를 조작하여 의미론적으로 유의미한 image interpolation이 가능하다. 반면, DDPM는 확률적 생성 과정(stochastic generative process)으로 인해 이미지 공간(image space) 근처에서만 보간이 이루어진다.
2 Background

주어진 데이터 분포 \( q(x_0) \)로부터 샘플을 생성할 수 있을 때, 본 연구에서는 \( q(x_0) \)를 근사하면서도 샘플링이 용이한 모델 분포 \( p_{\theta}(x_0) \)를 학습하는 데 관심이 있다. DDPM은 다음과 같은 형태의 latent variable model이다.

여기, \( x_1, \dots, x_T \)는 \( x_0 \)와 동일한 sample space (denoted as \( X \))에 속하는 잠재 변수들이다. 파라미터 \( \theta \)는 variational lower bound을 최대화하여 데이터 분포 \( q(x_0) \)에 맞도록 학습된다.

여기서 \( q(x_{1:T} | x_0) \)는 잠재 변수에 대한 어떠한 추론 분포(inference distribution)이다. 일반적인 잠재 변수 모델(예: VAE)과 달리, DDPM는 학습 가능한 추론 과정이 아니라 고정된 추론 과정 \( q(x_{1:T} | x_0) \)을 사용하며, 잠재 변수의 차원이 상대적으로 크다. 예를 들어, DDPM은 감소하는 시퀀스 \( \alpha_{1:T} \in (0,1]^T \)로 매개변수화된 Gaussian transitions를 가지는 다음과 같은 마르코프 체인을 고려하였다.

여기서 공분산 행렬의 대각 원소가 양수가 되도록 보장된다. 샘플링 절차가 autoregressive이므로, 이를 forward process 라 한다. 한편, \( p_{\theta}(x_{0:T}) \)은 \( x_T \)에서 \( x_0 \)로 샘플링하는 마르코프 체인으로 정의되며, 이는 생성 과정(generative process)이라 불린다. 생성 과정은 계산적으로 intractable한 역방향 과정 \( q(x_{t-1} | x_t) \)을 근사한다. 직관적으로, forward process은 관측값 \( x_0 \)에 점진적으로 잡음을 추가하는 반면, 생성 과정은 잡음이 추가된 관측값을 점진적으로 복원하는 역할을 한다(Figure 1, 왼쪽).
forward process의 특별한 성질 중 하나는 다음과 같다.

따라서 \( x_t \)는 \( x_0 \)와 잡음 변수 \( \epsilon \)의 선형 결합으로 표현할 수 있다.
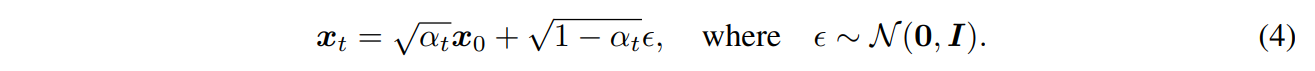
\( \alpha_T \)를 충분히 0에 가깝게 설정하면, \( q(x_T | x_0) \)는 모든 \( x_0 \)에 대해 표준 정규 분포로 수렴하므로, 자연스럽게 다음과 같이 설정할 수 있다. \(p_{\theta}(x_T) := \mathcal{N}(0, I)\). 모든 조건부 확률 \( p_{\theta}(x_{t-1} | x_t) \)을 가우시안 분포로 모델링하고, mean 함수는 학습 가능한 파라미터를 가지며 분산은 고정된 경우, 식 (2)의 목적 함수는 다음과 같이 단순화될 수 있다.

여기서, \( \epsilon_{\theta} := \{ \epsilon^{(t)}_{\theta} \}_{t=1}^{T} \)는 \( T \)개의 함수 집합이며, 각각 \( \epsilon^{(t)}_{\theta}: X \to X \)는 학습 가능한 파라미터 \( \theta^{(t)} \)를 포함하는 함수이다. 또한, \( \gamma := [\gamma_1, \dots, \gamma_T] \)는 목적 함수 내에서 \( \alpha_{1:T} \)에 따라 결정되는 양의 계수 벡터이다. DDPM에서는 \( \gamma = 1 \)로 설정한 목적 함수를 최적화하여 학습된 모델의 생성 성능을 극대화하였다. 이는 또한 noise conditional score networks (Song & Ermon, 2019)에서 사용된 목적 함수와 동일하며, score matching에 기반한다. 학습된 모델에서 \( x_0 \)를 샘플링하는 과정은 다음과 같다. 먼저, \( x_T \)를 사전 분포(prior) \( p_{\theta}(x_T) \)에서 샘플링한 후, 생성 과정(generative process)을 반복적으로 적용하여 \( x_{t-1} \)을 순차적으로 샘플링한다.
Forward process의 길이 \( T \)는 DDPM에서 중요한 하이퍼파라미터이다. 변분 관점에서 보면, \( T \)가 클수록 역방향 과정이 가우시안 분포에 가까워지며(Sohl-Dickstein et al., 2015), 따라서 가우시안 조건부 분포로 모델링된 생성 과정이 더 좋은 근사값을 제공하게 된다. 이러한 이유로, Ho et al. (2020)에서는 \( T = 1000 \)과 같은 큰 값을 선택하였다. 그러나 샘플 \( x_0 \)을 얻기 위해 \( T \)번의 iteration을 순차적으로 수행해야 하며, 병렬 처리가 불가능하다는 점이 문제로 작용한다. 이로 인해 DDPM에서의 샘플링 속도는 다른 딥 생성 모델보다 훨씬 느리며, 연산 자원이 제한적이거나 낮은 지연 시간(latency)이 중요한 작업에서는 실용성이 떨어진다.
3 Variational Inference For Non-Markovian Forward processes
생성 모델이 추론 과정(inference process)의 역(reverse)을 근사하기 때문에, 생성 모델이 필요한 반복(iterations) 수를 줄이려면 추론 과정을 다시 고찰할 필요가 있다. 본 논문의 핵심적인 관찰은 DDPM의 목적 함수 \( L_{\gamma} \)가 주변 분포 \( q(x_t | x_0) \)에만 의존하며, 결합 분포 \( q(x_{1:T} | x_0) \)에는 직접적으로 의존하지 않는다는 점이다. 따라서 동일한 주변 분포를 가지는 다양한 추론 분포(결합 분포)가 존재할 수 있으며, 이를 활용하여 non-Markovian 대안적인 추론 과정을 탐색할 수 있다. 이러한 접근 방식은 새로운 generative process을 유도하며(Figure 1, 오른쪽), 결과적으로 DDPM과 동일한 surrogate objective function를 얻을 수 있음을 본 논문에서 증명한다. 또한, Appendix A에서는 이러한 non-Markovian 관점이 가우시안 경우를 넘어 더 일반적인 경우에도 적용될 수 있음을 보인다.
3.1 Non-Markovian Forward Processes
추론 분포(inference distribution)의 집합 \( Q \)를 고려하자. 이는 실수 벡터 \( \sigma \in \mathbb{R}_{\geq 0}^{T} \)에 의해 인덱싱되며, 다음과 같이 정의된다.

여기서, \(q_{\sigma}(x_T | x_0) = \mathcal{N}(\sqrt{\alpha_T} x_0, (1 - \alpha_T)I)\)이며, 모든 \( t > 1 \)에 대해,
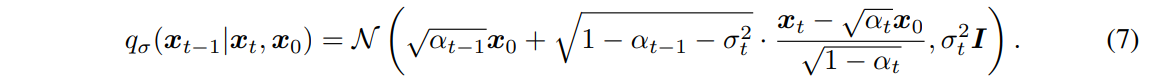
여기서 mean function은 \( q_{\sigma}(x_t | x_0) = \mathcal{N}(\sqrt{\alpha_t} x_0, (1 - \alpha_t)I) \)가 항상 성립하도록 설정된다(Appendix B의 Lemma 1 참조). 따라서 이는 원하는 주변 분포(marginals)와 일치하는 joint inference distribution를 정의한다. Forward process는 Bayes' rule를 통해 다음과 같이 유도할 수 있다.
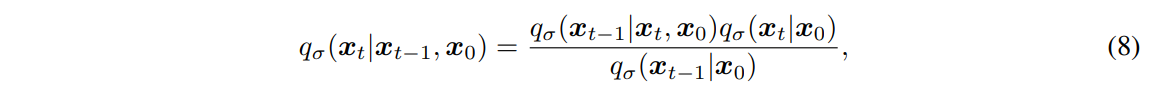
이 과정 또한 가우시안 분포를 따르지만, 본 논문에서는 이를 직접 활용하지 않는다. 식 (3)에서 정의된 확산 과정과 달리, 여기서의 forward process은 더 이상 Markovian process가 아니다. 이는 각 \( x_t \)가 \( x_{t-1} \)뿐만 아니라 \( x_0 \)에도 의존할 수 있기 때문이다. 또한, \( \sigma \)의 크기는 forward process의 확률적 성질을 조절하는 역할을 한다. 특히, \( \sigma \to 0 \)인 극한에서는 \( x_0 \)와 \( x_t \)를 알고 있는 경우, \( x_{t-1} \)이 고정된 값으로 결정되는 극단적인 경우가 된다.
3.2 Generative Process And Unified Variational Inference Objective
이제, 학습 가능한 생성 과정 \( p_{\theta}(x_{0:T}) \)을 정의하며, 여기서 각 \( p^{(t)}_{\theta}(x_{t-1} | x_t) \)는 \( q_{\sigma}(x_{t-1} | x_t, x_0) \)에 대한 정보를 활용한다. 직관적으로, noise가 포함된 관측값 \( x_t \)가 주어졌을 때, 먼저 이에 대응하는 \( x_0 \)을 예측한 후, 이를 이용하여 정의된 역방향 조건부 분포 \( q_{\sigma}(x_{t-1} | x_t, x_0) \)를 통해 \( x_{t-1} \)을 샘플링하는 방식이다.
일부 \( x_0 \sim q(x_0) \)와 \( \epsilon_t \sim \mathcal{N}(0, I) \)에 대해, \( x_t \)는 식 (4) \(x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon, \quad \text{where} \quad \epsilon \sim \mathcal{N}(0, I)\)를 이용하여 얻을 수 있다. 모델 \( \epsilon^{(t)}_{\theta}(x_t) \)는 \( x_0 \)를 알지 못한 상태에서 \( x_t \)로부터 \( \epsilon_t \)를 예측하려 한다. 식 (4)를 다시 정리하면, \( x_t \)가 주어졌을 때 잡음 제거된 관측값(즉, \( x_0 \)의 예측값)은 다음과 같이 표현할 수 있다.

이제, 고정된 사전 분포(prior) \( p_{\theta}(x_T) = \mathcal{N}(0, I) \)를 사용하여 생성 과정을 다음과 같이 정의할 수 있다.
(\( x_0 \)를 \( f^{(t)}_{\theta}(x_t) \)로 대체)

여기서, \( q_{\sigma}(x_{t-1} | x_t, f^{(t)}_{\theta}(x_t)) \)는 식 (7)에서 \( x_0 \)를 \( f^{(t)}_{\theta}(x_t) \)로 대체한 형태로 정의된다. 또한, \( t = 1 \)인 경우, 생성 과정이 모든 공간에서 유효하도록 보장하기 위해 Gaussian noise(공분산 \( \sigma_1^2 I \))을 추가한다.
파라미터 \( \theta \)는 다음과 같은 variational inference 목적 함수를 사용하여 최적화된다. (이는 함수적 표현을 통해 \( \epsilon_{\theta} \)에 대한 최적화를 수행함)

여기서 \( q_{\sigma}(x_{1:T} | x_0) \)는 식 (6)에 따라, \( p_{\theta}(x_{0:T}) \)는 식 (1)에 따라 인수분해된다.
\( J_{\sigma} \)의 정의만 보면, \( \sigma \)의 값이 달라질 때마다 서로 다른 variational objective가 생성되므로, \( \sigma \)의 각 선택마다 새로운 모델을 학습해야 할 것처럼 보인다. 이는 또한 서로 다른 생성 과정(generative process)에 대응한다. 그러나, 아래에서 보이듯이 \( J_{\sigma} \)는 특정 가중치 \( \gamma \)에 대해 \( L_{\gamma} \)와 동등하며, 따라서 동일한 목적 함수로 최적화될 수 있다.
Theorem 1. 모든 \( \sigma > 0 \)에 대해, 적절한 \( \gamma \in \mathbb{R}_{>0}^{T} \)와 상수 \( C \in \mathbb{R} \)가 존재하여, \(J_{\sigma} = L_{\gamma} + C\)가 성립한다.
변분 목적 함수 \( L_{\gamma} \)는 특수한 성질을 가지는데, 모델의 각 \( \epsilon^{(t)}_{\theta} \)에 대한 파라미터 \( \theta \)가 서로 다른 \( t \)에 대해 공유되지 않는다면, \( \epsilon_{\theta} \)의 최적 해(optimal solution)는 가중치 \( \gamma \)에 의존하지 않는다. 이는 \( L_{\gamma} \)의 각 항이 개별적으로 최적화될 때, 전역 최적(global optimum)이 독립적으로 달성될 수 있기 때문이다. 이러한 \( L_{\gamma} \)의 성질은 두 가지 중요한 함의를 가진다.
1. DDPM에서의 정당성: DDPM에서 variational lower bound에 대한 surrogate objective function으로 \( L_1 \)을 사용하는 것이 정당화된다.
2. \( J_{\sigma} \)와의 관계: Theorem 1에 따라 \( J_{\sigma} \)는 특정한 \( L_{\gamma} \)와 동등하므로, \( J_{\sigma} \)의 최적 해는 \( L_1 \)의 최적 해와 동일하다.
따라서, 모델의 \( \epsilon_{\theta} \)에서 \( t \) 간의 파라미터 공유가 없을 경우, DDPM에서 사용한 \( L_1 \) 목적 함수를 variational objective \( J_{\sigma} \)의 대리 함수로 사용할 수 있다.
4 Sampling From Generalized Generative Processes
\( L_1 \)을 목적 함수로 사용하면, 우리는 Sohl-Dickstein et al. (2015) 및 Ho et al. (2020)에서 고려한 Markovian 추론 과정에 대한 생성 과정(generative process)뿐만 아니라, 앞서 설명한 \( \sigma \)로 매개변수화된 다양한 non-Markovian forward process에 대한 생성 과정 또한 학습할 수 있다.
따라서, 사전 학습된 DDPM 모델을 새로운 목적 함수에 대한 solution으로 사용할 수 있으며, \( \sigma \)를 조정함으로써 우리의 필요에 맞게 샘플을 더 잘 생성할 수 있는 생성 과정을 찾는 데 집중할 수 있다.

4.1 Denoising Diffusion Implicit Models
식 (10)에서 정의된 \( p_{\theta}(x_{1:T}) \)를 사용하면, 주어진 샘플 \( x_t \)로부터 \( x_{t-1} \)을 다음과 같이 생성할 수 있다.

여기서 \( \epsilon_t \sim \mathcal{N}(0, I) \)는 \( x_t \)와 독립적인 표준 가우시안 잡음이며, \( \alpha_0 := 1 \)로 정의한다.
이 식에서 볼 수 있듯이, \( \sigma \)의 선택에 따라 서로 다른 생성 과정이 유도되지만, 동일한 모델 \( \epsilon_{\theta} \)을 사용할 수 있으므로 추가적인 재학습이 필요하지 않다. 즉, 사전 학습된 DDPM 모델을 그대로 사용하면서도, \( \sigma \) 값을 조정하여 더 적은 단계에서 효율적인 샘플링이 가능한 새로운 생성 과정을 설계할 수 있다.
특히, 모든 \( t \)에 대해 \(\sigma_t = \sqrt{\frac{(1 - \alpha_{t-1})}{(1 - \alpha_t)} \cdot \frac{1 - \alpha_t}{\alpha_{t-1}}}\)로 설정하면, forward process가 Markovian process가 되며, 생성 과정이 DDPM과 동일하게 된다.
특히, \( \sigma_t = 0 \)인 경우(모든 \( t \)에 대해) 또 다른 중요한 사례가 존재한다. 이 경우, forward process는 deterministic이 되어, \( x_{t-1} \)과 \( x_0 \)가 주어지면 \( x_t \)가 유일하게 결정된다(단, \( t = 1 \)에서는 예외적으로 무작위성이 존재할 수 있음). Generative process에서는 random noise \( \epsilon_t \) 앞의 계수가 0이 되어, 샘플링 과정에서 확률적 요소가 사라진다. 즉, 확률적 샘플링이 아니라, 고정된 절차(fixed process)에 따라 \( x_T \)에서 \( x_0 \)으로 변환되는 구조가 된다. 이러한 특성을 가지는 모델을 denoising diffusion implicit model (DDIM)이라 명명하며, 이는 DDPM의 목적 함수로 학습되었지만, 순방향 과정이 더 이상 확산(diffusion) 과정이 아닌 암시적 확률 모델로 동작한다. DDIM은 DDPM과 같은 학습 과정을 따르면서도, 샘플링 속도를 극적으로 향상시킬 수 있는 모델이다.
4.2 Accelerated Generation Processes
이전 섹션들에서는 generative process가 reverse process의 근사로 간주되었으며, forward process가 \( T \) 단계로 이루어지므로 generative process도 \( T \) 단계에서 샘플링을 수행해야 했다.
그러나 denoising objective \( L_1 \)은 특정한 forward process에 직접적으로 의존하지 않으며, 단 \( q_{\sigma}(x_t | x_0) \)가 고정되어 있기만 하면 된다. 따라서, 반드시 \( T \) 단계의 forward process순방향 과정을 따를 필요가 없으며, \( T \)보다 짧은 길이의 forward process도 고려할 수 있다. 이렇게 하면, generative process에서 필요한 샘플링 단계를 줄여 샘플링 속도를 가속할 수 있으며, 기존 모델을 재학습할 필요 없이 바로 적용 가능하다.
Forward process를 모든 잠재 변수 \( x_{1:T} \)에 대해 정의하는 것이 아니라, 특정 부분집합 \( \{ x_{\tau_1}, \dots, x_{\tau_S} \} \)에 대해 정의하는 방식을 고려하자. 여기서 \( \tau \)는 길이 \( S \)의 증가하는 부분 수열이며, \( \tau \subseteq [1, \dots, T] \)을 만족한다. 특히, sequential forward process를 다음과 같이 정의한다. \(q(x_{\tau_i} | x_0) = \mathcal{N}(\sqrt{\alpha_{\tau_i}} x_0, (1 - \alpha_{\tau_i}) I)\). 즉, 이 과정은 기존의 \( q(x_t | x_0) \)와 동일한 주변 분포를 유지하도록 설계된다(Figure 2 참조). generative process에서는 이제 역순으로 정렬된 \( \tau \)의 인덱스(reversed(\( \tau \)))에 따라 잠재 변수를 샘플링하며, 이를 "샘플링 경로(sampling trajectory)"라고 부른다. 샘플링 경로의 길이가 \( T \)보다 훨씬 작을 경우, 샘플링 과정의 iteration 횟수가 줄어들어 computational efficiency가 크게 향상될 수 있다. 이는 샘플링이 점진적으로 이루어지는 구조(iterative nature)를 활용하여 성능을 개선하는 핵심적인 기법이다. 즉, 사전 학습된 DDPM 모델을 활용하면서도, 샘플링 속도를 최적화할 수 있는 새로운 생성 과정 설계가 가능해진다.
Section 3에서와 유사한 논리를 적용하면, \( L_1 \) 목적 함수로 학습된 모델을 그대로 사용할 수 있으므로, 별도의 재학습이 필요하지 않다. 즉, 모델 학습 과정에는 변화가 없으며, 단순히 generative process에서 일부 업데이트를 수정하는 것만으로 새로운, 더 빠른 생성 과정을 구현할 수 있다. 특히, 식 (12)에서의 업데이트를 약간만 변경하면, DDPM, DDIM뿐만 아니라 식 (10)에서 고려된 모든 생성 과정에도 적용할 수 있다. 즉, 동일한 학습된 모델을 활용하면서도, 다양한 샘플링 전략을 통해 더 효율적인 샘플링을 수행할 수 있다. 이와 관련된 세부 사항은 Appendix C.1**에서 다루며, 여기서 새로운 샘플링 기법을 적용하는 구체적인 방법을 설명한다.
이론적으로, forward process의 단계 수를 임의로 설정하여 모델을 학습한 후, generative process에서는 일부 단계만 선택하여 샘플링할 수 있다. 즉, 학습된 모델은 전체 \( T \) 단계의 순방향 과정을 고려할 수 있지만, 실제 샘플링에서는 더 적은 단계만을 활용하여 효율적인 생성이 가능하다. 따라서, Ho et al. (2020)에서 고려한 단계 수보다 훨씬 많은 단계로 모델을 학습하거나, 심지어 연속적인 시간 변수 \( t \)를 사용하는 접근법(Chen et al., 2020)도 가능하다. 이는 생성 과정의 유연성을 극대화할 수 있는 가능성을 열어준다. 이러한 방향의 실험적 검증은 향후 연구 과제로 남긴다.
4.3 Relevance To Neural ODEs
또한, DDIM의 반복을 식 (12)에 따라 다시 정리하면, 이는 상미분 방정식(ordinary differential equations, ODE)을 푸는 오일러 적분(Euler integration)과 유사함이 더욱 명확해진다.

이를 기반으로 해당하는 ODE를 유도하기 위해, \( \sqrt{(1 - \alpha) / \alpha} \)를 \( \sigma \)로, \( x / \sqrt{\alpha} \)를 \( \bar{x} \)로 reparameterize할 수 있다. 연속적인 경우, \( \sigma \)와 \( x \)는 시간 \( t \)의 함수가 되며, \(\sigma: \mathbb{R}_{\geq 0} \to \mathbb{R}_{\geq 0}\)는 연속적이고 증가하는 함수이며, \( \sigma(0) = 0 \)을 만족한다. 이때, 식 (13)은 다음 ODE에 대한 오일러 방법(Euler method)으로 해석할 수 있다.

여기서 초기 조건은 \( \sigma(T) \)가 충분히 크면 \( x(T) \sim \mathcal{N}(0, \sigma(T)) \)가 된다. 이는 \( \alpha \approx 0 \)**인 경우에 해당한다. 이러한 해석은 중요한 시사점을 제공한다.
1. 충분한 이산화(discretization) 단계가 주어진다면, 생성 과정(reverse generation process)은 ODE의 역(reverse)을 시뮬레이션하는 과정으로 볼 수 있다. 즉, \( t = 0 \)에서 \( T \)까지 진행하는 forward process가 \( x_0 \)에서 \( x_T \)로 인코딩하는 과정이 되며, 이는 ODE의 역을 푸는 것과 동일한 의미를 갖는다.
2. DDIM은 DDPM과 달리, 생성 과정뿐만 아니라 입력 관측값을 latent representation으로 변환하는 기능을 제공할 수 있다. 즉, 모델의 잠재 표현으로서 \( x_T \) 형태의 인코딩을 얻을 수 있으며, 이는 downstream task에서도 활용될 수 있는 가능성을 제공한다. 예를 들어, 이미지 표현 학습, 생성 모델 기반 feature extraction 등의 응용에 유용할 수 있다.
Song et al. (2020)의 동시 연구(concurrent work)에서는, 확률 흐름 ODE(probability flow ODE)를 제안하여 확률적 미분 방정식(SDE)의 주변 밀도(marginal densities)를 점수(scores)를 기반으로 복원하는 방법을 제시하였다. 이 접근 방식은 DDPM과 유사한 샘플링 스케줄을 유도할 수 있다. 여기서, 본 논문의 ODE는 Song et al. (2020)의 "Variance-Exploding" SDE에 대응하는 특수한 경우와 동등함을 보인다.
Proposition 1. 식 (14)의 ODE는 최적 모델 \( \epsilon^{(t)}_{\theta} \)을 사용할 경우, Song et al. (2020)에서 제안한 "Variance-Exploding" SDE에 해당하는 확률 흐름 ODE(probability flow ODE)와 동등하다.
이에 대한 증명은 Appendix B에 포함되어 있다. ODE는 동일하지만, 샘플링 절차는 다르다. 비록 ODE 자체는 동일하지만, 샘플링 방식에서 차이가 존재한다. Song et al. (2020)의 확률 흐름 ODE에서 오일러 방법(Euler method)을 적용하면 다음과 같은 업데이트가 이루어진다.

이 식은 \( \alpha_t \)와 \( \alpha_{t - \Delta t} \)가 충분히 가까운 경우, 본 논문에서 제안한 업데이트 식과 동일해진다. 그러나, 샘플링 단계 수가 적을 경우, 두 방법 간의 차이가 발생할 수 있다. 본 논문에서는 \( d\sigma(t) \)를 기준으로 오일러 스텝을 수행한다. \( d\sigma(t) \)는 "시간" \( t \)의 스케일링과 직접적인 영향을 받지 않는다. 반면, Song et al. (2020)의 접근 방식은 \( dt \)를 기준으로 오일러 스텝을 적용한다. 따라서, 동일한 ODE를 기반으로 하더라도 샘플링 속도와 품질 측면에서 차이가 있을 수 있으며, 샘플링 효율을 높이기 위한 최적의 접근 방식은 다를 수 있다.
5 Experiments
본 섹션에서는 DDIMs가 적은 반복(iterations) 수를 사용할 경우 DDPMs보다 뛰어난 이미지 생성 성능을 보이며, DDPM의 원래 생성 과정보다 10배에서 100배까지 빠른 속도를 제공함을 보인다. 또한, DDIMs는 DDPMs와 달리, 초기 잠재 변수 \( x_T \)가 고정되었을 때, 생성 경로(generation trajectory)에 상관없이 고수준(high-level) 이미지 특징을 유지하는 특성을 가진다. 이로 인해 잠재 공간(latent space)에서 직접 보간(interpolation)을 수행할 수 있다. 또한, DDIMs는 샘플을 인코딩하여(latent code로 변환) 원래 이미지를 복원하는 기능을 제공할 수 있다. 즉, 이미지를 DDIM의 잠재 공간에 매핑한 후, 이를 다시 원본 이미지로 복원할 수 있는 구조를 갖는다.
각 데이터셋에 대해, \( T = 1000 \)으로 학습된 동일한 모델을 사용하며, 목적 함수는 식 (5)의 \( L_{\gamma} \)이며 \( \gamma = 1 \)로 설정된다. Section 3에서 논의한 바와 같이, 학습 절차에는 변경이 필요하지 않다. 유일한 변경 사항은 모델에서 샘플을 생성하는 방식이다. 이를 위해 다음 두 가지를 조절한다.
1. \( \tau \) (샘플링 속도 조절):
- \( \tau \)는 샘플이 생성되는 속도를 조절하며, 이를 통해 더 적은 반복(iterations)으로 샘플링 속도를 높일 수 있다.
2. \( \sigma \) (결정론적 DDIM과 확률적 DDPM 사이의 조절):
- \( \sigma \)는 결정론적 DDIM과 확률적 DDPM 사이를 보간(interpolate)하는 역할을 한다.
- \( \sigma = 0 \)이면 DDIM처럼 동작하여 결정론적(deterministic) 샘플링을 수행한다.
- \( \sigma > 0 \)이면 DDPM처럼 동작하여 확률적(stochastic) 샘플링을 수행한다.
이러한 조절을 통해, 동일한 학습된 모델을 유지하면서도 샘플링 속도 및 특성을 사용자 요구에 맞게 조정할 수 있다.
우리는 다양한 부분 수열 \( \tau \) (즉, \( [1, \dots, T] \)의 일부 요소들로 구성된 샘플링 경로)과 다양한 분산 하이퍼파라미터 \( \sigma \)를 고려한다. 여기서 \( \sigma \)는 \( \tau \)의 요소들에 따라 결정되며, 다음과 같은 형태로 설정된다.

여기서 \( \eta \geq 0 \)는 직접 조정 가능한 하이퍼파라미터이다. \( \eta = 1 \)이면 기존 DDPM 생성 과정과 동일한 방식이 된다. \( \eta = 0 \)이면 DDIM 생성 과정이 되어 결정론적(deterministic) 샘플링이 이루어진다. 또한, DDPM에서 랜덤 잡음의 표준 편차가 기존 \( \sigma(1) \)보다 큰 경우도 고려하며, 이를 \( \hat{\sigma} \)로 표기한다. \( \hat{\sigma}_{\tau_i} = \sqrt{\frac{1 - \alpha_{\tau_i}}{\alpha_{\tau_i - 1}}} \). 이는 Ho et al. (2020)의 구현에서 CIFAR-10 샘플을 얻을 때만 사용되었으며, 다른 데이터셋에는 적용되지 않았다. 이와 관련된 추가적인 세부 사항은 Appendix D에서 다룬다.
5.1 Sampling Quality and Efficency

Table 1에서는 CIFAR10과 CelebA 데이터셋에서 학습된 모델을 사용하여 생성된 샘플의 품질을 Frechet Inception Distance (FID (Heusel et al., 2017))로 측정하여 보고한다. 여기서 샘플을 생성하는 데 사용된 timestep의 수 \(\dim(\tau)\) 및 과정의 확률성 \(\eta\)를 변화시켰다. 예상대로, \(\dim(\tau)\)가 증가함에 따라 샘플 품질이 향상되며, 이는 샘플 품질과 계산 비용 간의 트레이드오프를 나타낸다. 우리는 \(\dim(\tau)\)가 작은 경우 DDIM (\(\eta = 0\))이 가장 우수한 샘플 품질을 달성하며, DDPM (\(\eta = 1\) 및 \(\hat{\sigma}\))은 동일한 \(\dim(\tau)\)에서 더 확률성이 낮은 모델들보다 일반적으로 샘플 품질이 떨어지는 것을 관찰한다. 다만, Ho et al. (2020)에서 보고한 \(\dim(\tau) = 1000\) 및 \(\hat{\sigma}\)의 경우에는 DDIM이 약간 더 나쁜 성능을 보였다. 그러나 \(\dim(\tau)\)가 작아질수록 \(\hat{\sigma}\)의 샘플 품질은 훨씬 더 저하되며, 이는 짧은 생성 경로에서는 부적절할 수 있음을 시사한다. 반면, DDIM은 보다 일관되게 높은 샘플 품질을 달성한다.

Figure 3에서는 동일한 샘플링 단계 수에서 \(\sigma\)를 변화시키며 생성된 CIFAR10 및 CelebA 샘플을 보여준다. DDPM의 경우, 샘플링 경로가 10단계일 때 샘플 품질이 급격히 저하된다. \(\hat{\sigma}\)의 경우, 생성된 이미지가 짧은 경로에서 더 많은 노이즈성 섭동을 포함하는 것으로 보이며, 이는 FID 점수가 다른 방법들보다 훨씬 나쁜 이유를 설명한다. 이는 FID가 이러한 perturbations에 매우 민감하기 때문이며, 이에 대해서는 Jolicoeur-Martineau et al. (2020)에서 논의되었다.
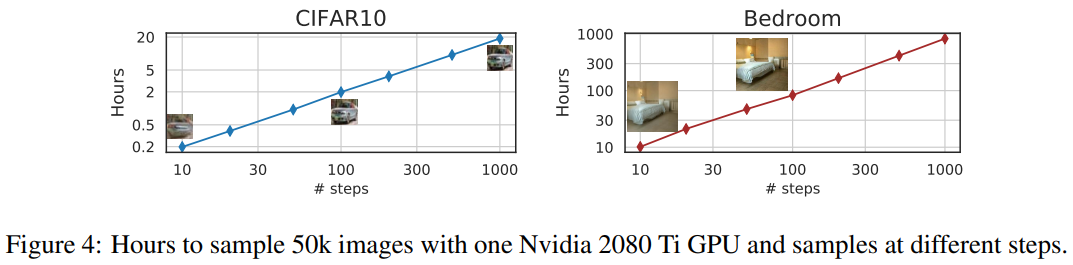
Figure 4에서는 샘플을 생성하는 데 필요한 시간이 샘플 경로의 길이에 선형적으로 비례함을 보여준다. 이는 DDIM이 훨씬 적은 단계로 샘플을 생성할 수 있어 보다 효율적인 샘플링이 가능함을 시사한다. 특히, DDIM은 20~100 단계 내에서 1000단계 모델과 비교할 만한 품질의 샘플을 생성할 수 있으며, 이는 기존 DDPM 대비 10배에서 50배의 속도 향상을 의미한다. DDPM 또한 100단계로도 적절한 샘플 품질을 달성할 수 있지만, DDIM은 이를 훨씬 적은 단계로 달성할 수 있다. 예를 들어, CelebA 데이터셋에서 100단계 DDPM의 FID 점수는 20단계 DDIM과 유사하다.
5.2 Sampling Consistency In DDIM

DDIM의 경우 생성 과정이 결정론적이며, \( x_0 \)는 오직 초기 상태 \( x_T \)에만 의존한다. Figure 5에서 우리는 동일한 초기 \( x_T \)에서 시작하되, 서로 다른 생성 경로(즉, 서로 다른 \( \tau \)를 사용)에서 생성된 이미지를 관찰한다. 흥미롭게도, 동일한 초기 \( x_T \)에서 생성된 이미지들은 생성 경로와 관계없이 대부분의 high-level 특징이 유사하게 유지된다. 많은 경우, 단 20단계만을 사용하여 생성된 샘플조차도 1000단계에서 생성된 샘플과 비교할 때 high-level 특징이 거의 동일하며, 세부적인 차이만 존재한다. 따라서 \( x_T \)만으로도 이미지의 유익한 잠재 인코딩 역할을 할 수 있으며, 샘플 품질에 영향을 미치는 미세한 세부 정보는 파라미터에 의해 결정된다고 볼 수 있다. 즉, 더 긴 샘플 경로를 사용할수록 품질이 향상되지만, high-level 특징에는 큰 영향을 미치지 않는다. 추가적인 샘플은 Appendix D.4에 제시하였다.

DDIM 샘플의 고수준 특징이 \( x_T \)에 의해 인코딩되므로, 우리는 이것이 다른 암시적 확률 모델(예: GAN)에서 관찰된 것과 유사한 semantic interpolation 효과를 나타내는지 확인하고자 한다. 이는 Ho et al. (2020)에서 제안한 보간(interpolation) 방법과는 다르다. DDPM에서는 확률적 생성 과정으로 인해 동일한 \( x_T \)에서 매우 다양한 \( x_0 \)가 생성될 수 있기 때문이다. Figure 6에서는 \( x_T \)에서의 단순한 보간이 두 샘플 간 의미론적으로 유의미한 변화를 유도할 수 있음을 보여준다. 추가적인 세부 정보와 샘플들은 Appendix D.5에 포함되어 있다. 이는 DDIM이 잠재 변수를 통해 생성된 이미지의 고수준 특징을 직접적으로 제어할 수 있도록 하며, 이는 DDPM에서는 불가능한 점이다.
5.4 Reconstruction From Latent Space

DDIM이 특정 ODE에 대한 오일러 적분(Euler integration)이라는 점에서, \( x_0 \)에서 \( x_T \)로의 인코딩(Equation (14)의 역방향)과, 생성된 \( x_T \)에서 다시 \( x_0 \)로의 복원(Equation (14)의 정방향)이 가능한지 살펴보는 것은 흥미로운 문제이다. 우리는 CIFAR-10 모델을 사용하여 CIFAR-10 테스트에서 \( S \) 단계의 인코딩 및 디코딩을 수행하며, 각 차원당 평균 제곱 오차(mean squared error)를 [0,1] 범위로 스케일링하여 Table 2에 보고한다. 실험 결과, \( S \) 값이 클수록 DDIM의 reconstruction error가 낮아지며, 이는 Neural ODE 및 normalizing flow와 유사한 성질을 나타낸다. 반면, DDPM은 확률적 생성 과정으로 인해 동일한 특성을 가지지 않는다.
6 Related Works
본 연구는 생성 모델을 마르코프 체인의 전이 연산자로 학습하는 기존 방법들의 광범위한 계열을 기반으로 한다 (Sohl-Dickstein et al., 2015; Bengio et al., 2014; Salimans et al., 2014; Song et al., 2017; Goyal et al., 2017; Levy et al., 2017). 이들 중에서도, denoising diffusion probabilistic models (DDPMs, Ho et al. (2020))과 noise conditional score networks (NCSN, Song & Ermon (2019; 2020))는 최근 높은 샘플 품질을 달성하여 GANs (Brock et al., 2018; Karras et al., 2018)과 비교할 만한 성능을 보였다. DDPM는 log-likelihood의 variational lower bound을 최적화하는 반면, NCSN는 데이터의 비모수적 Parzen 밀도 추정기(Parzen density estimator)에 대한 score matching objective (Hyvärinen, 2005)를 최적화한다 (Vincent, 2011; Raphan & Simoncelli, 2011).
DDPM와 NCSN는 서로 다른 동기에서 출발했지만, 두 방법은 밀접한 관련이 있다. 두 모델 모두 여러 수준의 노이즈에 대해 denoising autoencoder objective를 사용하며, 샘플을 생성하는 과정에서 Langevin dynamics와 유사한 절차를 따른다 (Neal et al., 2011). Langevin dynamics는 gradient flow의 이산화(discretization) 과정이므로 (Jordan et al., 1998), DDPM과 NCSN 모두 높은 샘플 품질을 얻기 위해 많은 단계가 필요하다. 이는 DDPM 및 기존 NCSN 방법들이 적은 반복(iteration) 내에서 고품질 샘플을 생성하는 데 어려움을 겪는다는 관찰 결과와 일치한다.
반면, DDIM은 잠재 변수로부터 샘플이 고유하게 결정되는 implicit generative model이다. 따라서, DDIM은 의미론적으로 유의미한 보간(interpolation)을 생성할 수 있는 능력과 같은 특성을 가지며, 이는 GAN 및 invertible flows과 유사하다. 우리는 순수하게 variational 관점에서 DDIM을 유도하였으며, 이 과정에서 Langevin dynamics의 제약은 고려되지 않는다. 이러한 점은 적은 iteration에서도 DDPM보다 우수한 샘플 품질을 얻을 수 있었던 이유를 부분적으로 설명할 수 있다. 또한, DDIM의 샘플링 과정은 연속적인 깊이를 가지는 신경망(neural networks with continuous depth)과 유사한 특징을 보인다. 즉, 동일한 잠재 변수에서 생성된 샘플들은 특정 샘플링 경로와 관계없이 유사한 고수준 시각적 특징을 유지한다.
7 Discussion
우리는 denoising auto-encoding 및 score matching objective로 학습된 암시적 생성 모델인 DDIM을 순수한 변분적(variational) 관점에서 제시하였다. DDIM은 기존 DDPM 및 NCSN보다 훨씬 효율적으로 고품질 샘플을 생성할 수 있으며, 잠재 공간에서 의미론적으로 유의미한 보간(interpolation)을 수행할 수 있는 능력을 갖추고 있다.
본 논문에서 제시한 비마르코프(Non-Markovian) 정방향 과정은, 원래의 diffusion framework에서는 사용할 수 없는 가우시안 이외의 연속적인 정방향 과정이 가능함을 시사한다. 이는 가우시안 분포가 유한 분산을 가지는 유일한 안정적 분포이기 때문이다. 또한, Appendix A에서 다항(multinomial) 정방향 과정을 포함한 이산적(discrete) 사례를 제시하였으며, 이를 다른 조합론적(combinatorial) 구조에도 확장하는 것이 흥미로운 연구 방향이 될 것이다.
더 나아가, DDIM의 샘플링 과정이 신경 ODE(neural ODE)와 유사하다는 점을 고려할 때, ODE의 이산화 오류(discretization error)를 줄이는 방법이 DDIM의 성능 향상에 기여할 수 있는지 검토하는 것도 흥미로운 연구 주제이다. 예를 들어, Adams-Bashforth (Butcher & Goodwin, 2008)와 같은 multistep 방법이 적은 단계에서 샘플 품질을 더욱 향상시키는 데 유용할 수 있다 (Queiruga et al., 2020). 또한, DDIM이 기존 implicit models의 다른 특성을 보이는지 연구하는 것도 의미 있는 방향이 될 것이다 (Bau et al., 2019).
'논문 리뷰 > Generative models' 카테고리의 다른 글
| DDPM Loss Function 요약 설명 (0) | 2025.03.09 |
|---|---|
| [논문 리뷰] Classifier-Free Diffusion Guidance (0) | 2025.03.06 |
| [논문 리뷰] Diffusion Models Beat GANs on Image Synthesis (0) | 2025.03.05 |
| [논문 리뷰] MangaNinja: Line Art Colorization with Precise Reference Following (0) | 2025.02.18 |
| [논문 리뷰] IP-Adapter: Text Compatible Image Prompt Adapter for Text-to-Image Diffusion Models (0) | 2025.01.10 |




